State estimators and observers for continuous and discrete linear systems
Part 1. Differential asymptotic state estimators
DOI:
https://doi.org/10.5604/01.3001.0012.8169Słowa kluczowe:
linear estimators, Kalman filter, Luenberger observer, exact state observers, linear systemsAbstrakt
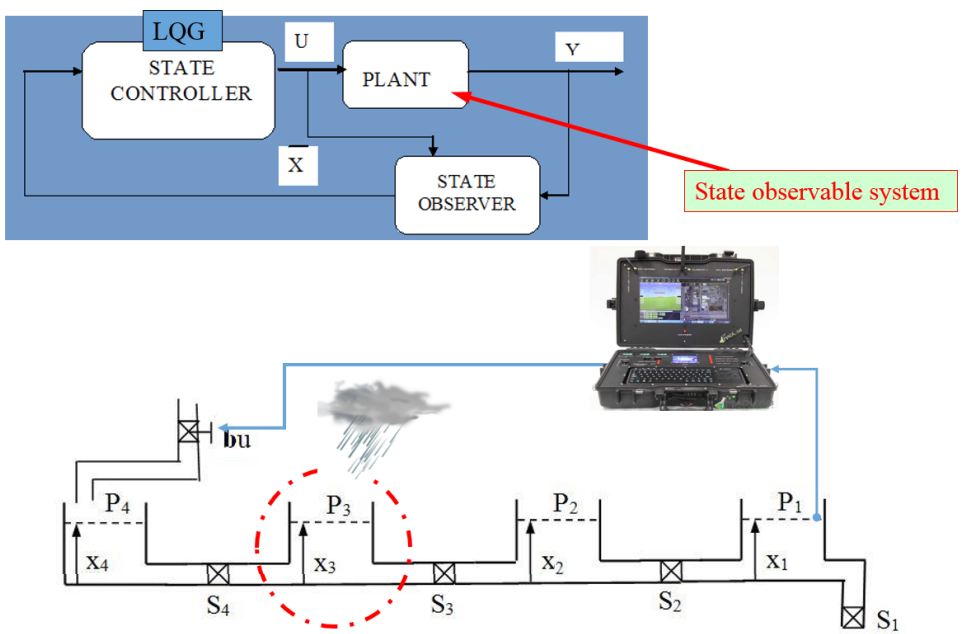
In the paper an overview of state estimators and state observers used in linear systems, will be presented. The state estimators and observers can be used in many applications like the state reconstruction for the control purposes or for the diagnosis and fault detection in technical processes or for the virtual measurements of inaccessible variables of the system as well as for the best filtration of the differential equation solution. As the standard most commonly the Kalman filter and Luenberger type observers are used. Although the Kalman filter guarantees optimal filtering quality of the state, reconstructed from the noisy measurements, both Kalman filter and the Luenberger observer guarantee only asymptotic quality of the real state changes and tracking, basing on the current measurements of the system output and input signals. Unfortunately, the value of the estimation error at any moment of time cannot be calculated. The discussion on differences between continuous and two types of discrete Kalman Filter will be presented. This paper is plan to be the introduction to presentation of the another type of the state observers which have the structure given by the integral operators. Based on measurements of the system output and input signals on some predefined finite time interval, they can reconstruct, after this interval, the observed state exactly.
Statystyka pobrań
Bibliografia
Kalman R, Contribution to the theory of optimal control. Conf. on Ordinary Differential Equation. Mexico City, Bol. Soc. Mat. Mex. 1960; 5:102–119. Google Scholar
Kalman R, A new approach to linear filtering and prediction problems, Journal of Basic Engineering, 1960; 82(1):35–45. Google Scholar
Kalman R, Bucy R, New results in linear filtering and prediction theory, Journal of Basic Eng. Transaction of ASME, 1961; 83D:95–108. Google Scholar
Luenberger D, Observers for multivariable systems. IEEE Transactions on Automatic Control, 1966; 11:190–197. Google Scholar
Kwakernaak H, Sivan R, Linear Optimal Control Systems, Wiley, 1972. Google Scholar
Nazarzadeh J, Razzaghi M, Nikravesh KY, Solution of the Matrix Riccati Equation for the Linear Quadratic Control Problems, Math. Comput. Modeling, 1998; 27(7):51–55. Google Scholar
Ledyaev YS, On analytical solution of matrix Riccati equations, Proceedings of the Steklov Institute of Mathematics, 2011; 273(1):214–228. Google Scholar
Franklin G, Powell D, Workman M, Digital Control of Dynamic System. Addison Wesley,1990. Google Scholar
Chui CK, Chen G, Kalman Filtering with Real-time Applications, Second Edition, Springer-Verlag, Berlin, 1991. Google Scholar
Pobrania
Opublikowane
Jak cytować
Numer
Dział
Licencja
Prawa autorskie (c) 2018 Państwowa Wyższa Szkoła Zawodowa w Tarnowie & Autorzy

Utwór dostępny jest na licencji Creative Commons Uznanie autorstwa – Użycie niekomercyjne 4.0 Międzynarodowe.



