A remark on the distribution of products of independent normal random variables
DOI:
https://doi.org/10.5604/01.3001.0014.7861Keywords:
normal distribution, Maijer G-functionsAbstract
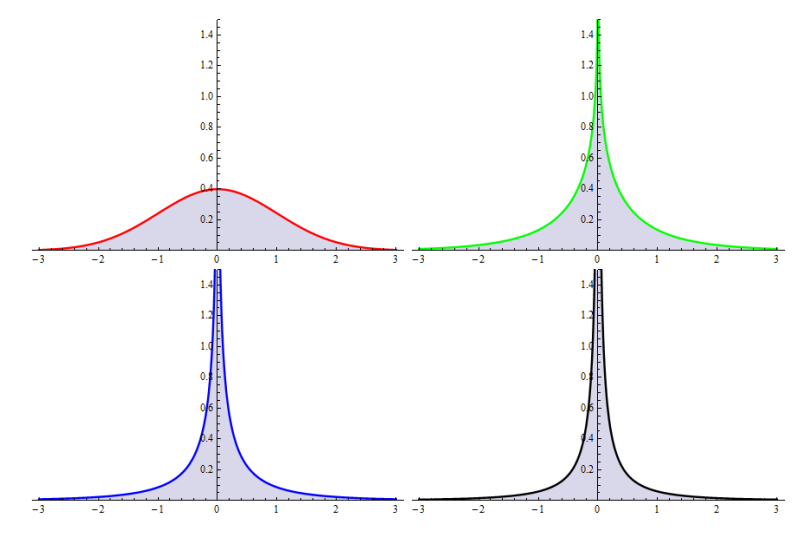
We present a proof of the explicit formula of the probability density function of the product of normally distributed independent random variables using the multiplicative convolution formula for Meijer G functions.
Downloads
References
Bateman H, Erdélyi A. Higher transcendental functions. Vol. 1. New York: McGraw-Hill; 1953. Google Scholar
Beals R, Szmigielski J. Meijer G-functions: a gentle introduction. Notices of the American Mathematical Society. 2013;60(7):866–872. doi: http://dx.doi.org/10.1090/notimanid1016. Google Scholar
Carter BD, Springer MD. The distribution of products, quotients and powers of independent H-function variates. SIAM Journal on Applied Mathematics. 1977;33(4):542–558. doi: https://doi.org/10.1137/0133036. Google Scholar
Craig CC. On the frequency function of XY. The Annals of Mathematical Statistics. 1936;7(1):1–15. Google Scholar
Craig CC. On frequency distributions of the quotient and of the product of two statistical variables. The American Mathematical Monthly. 1942;49(1):24–32. doi: https://doi.org/10.1080/00029890.1942.11991175. Google Scholar
Fisz M. Probability and Mathematical Statistics. Delhi: S. Chand; 1961. Google Scholar
Gradshteyn IS, Ryzhik IM. Table of Integrals, Series, and Products. 7th ed. Amsterdam: Academic Press; Elsevier; 2007. Google Scholar
Springer MD. The Algebra of Random Variables. Wiley Series in Probability and Mathematical Statistics. New York–Chichester–Brisbane: John Wiley & Sons; 1979. Google Scholar
Springer MD, Thompson WE. The distribution of products of independent random variables. SIAM Journal on Applied Mathematics. 1966;14(3):511–526. doi: https://doi.org/10.1137/0114046. Google Scholar
Springer MD, Thompson WE. The distribution of products of beta, gamma and Gaussian random variables. SIAM Journal on Applied Mathematics. 1970;18(4):721–737. doi: https://doi.org/10.1137/0118065. Google Scholar
Wishart J, Barlett MS. The distribution of second order moment statistics in a normal system. Mathematical Proceedings of the Cambridge Philosophical Society. 1932;28(4):455–459. doi: https://doi.org/10.1017/S0305004100010690. Google Scholar
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2021 University of Applied Sciences in Tarnow, Poland & Author

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.



